Research — Reach-Avoid Games
Starting in August of 2020, I worked as a student researcher with Dr. Yancy Diaz-Mercado of the UMD Collaborative Controls and Robotics Lab. In my work, I investigated the control of a team of pursuer agents so as to guarantee capture of a faster, lone evader agent. The work resulted in the development of an improved distributed pursuer control algorithm and a set of closed form expressions for the number of pursuers needed for the geometric feasibility of capture, as well as simulation and realtime implementation in MATLAB. The results were presented at and published in the proceedings of the 2021 Modeling, Estimation, and Controls Conference (MECC2021).
Background
In a reach-avoid game, one or more "evader" agents attempts to reach a certain target set, while avoiding capture by one or more "pursuer" agents. These sorts of games had previously been studied in the case where the pursuers are faster than the evader, and where the pursuer and evader have equal speed. My work focused specifically on the case of a single fast evader avoiding many slow pursuers in a time-bounded game, and on developing both a control system for the pursuers and some sort of bound on how many pursuers are actually needed.
Theoretical Work and Simulation
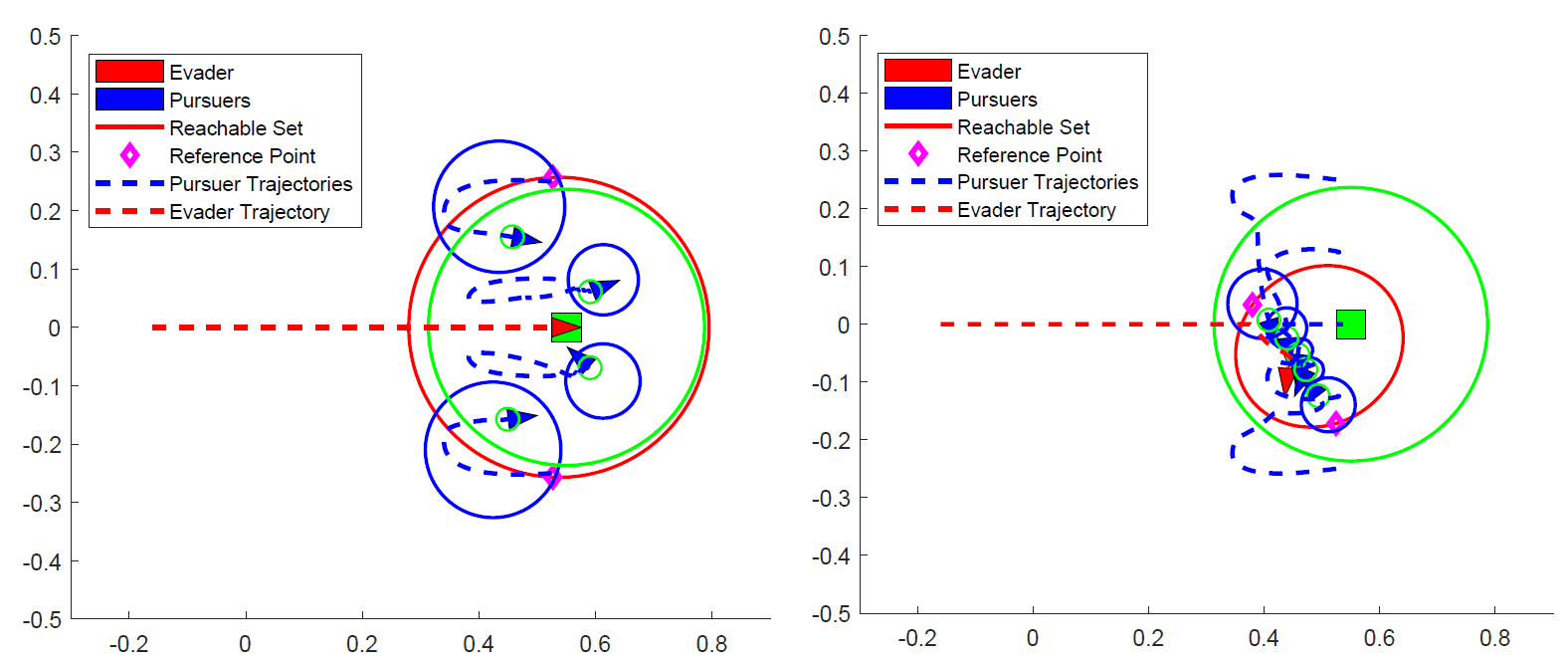
My results were derived from previous work by Alexander Davydov which showed that capture could be guaranteed if the pursuers followed a Control Barrier Function (CBF) controller, so long as solving under the appropriate constraints was feasible. However, the previous work did not formulate a way to tell if there existed a feasible solution in a given situation.
I developed a set of equations arising from geometric constraints that gave the minimum number of agents sufficient for geometric feasibility. I then verified these equations in simulation, showing capture to always occur provided at least the number of agents given by the above expressions was used.
Experiment
Finally, we needed to show that the proposed controller was not only possible in simulation, but actually practical to run on real robots. To that end, we optimized the solvers we used by linearizing our constraints (conservatively) and applying the fastest solvers wherever possible.
The resulting controller was then implemented on a team of Khepera unicycle robots, which ran it in real time.
Publication
The results of this research were accepted for presentation at the 2021 Modeling, Estimation, and Controls Conference (Oct. 25th-27th, 2021) and can be found at the conference site once available.